¶ Erstbewertung der Parametervariabilität (a-priori-Verteilungen) bei geringer standortspezifischer Informationslage
¶ Mitwirkende:
- Chair of Numerical Analysis (Technical University of Chemnitz): Chao Chang, Oliver Ernst, Moritz Poguntke
- Department Underground Space for Storage and Economic Use - Sub-department Rock Characterisation for Storage and Final Disposal (Federal Institute for Geosciences and Natural Resources): Werner Gräsle, Sibylle Mayr
- Chair of Soil Mechanics and Foundation Engineering (Technical University of Bergakademie Freiberg): Aqeel Afzal Chaudhry, Thomas Nagel
¶ Ursprung der Parameterunsicherheiten
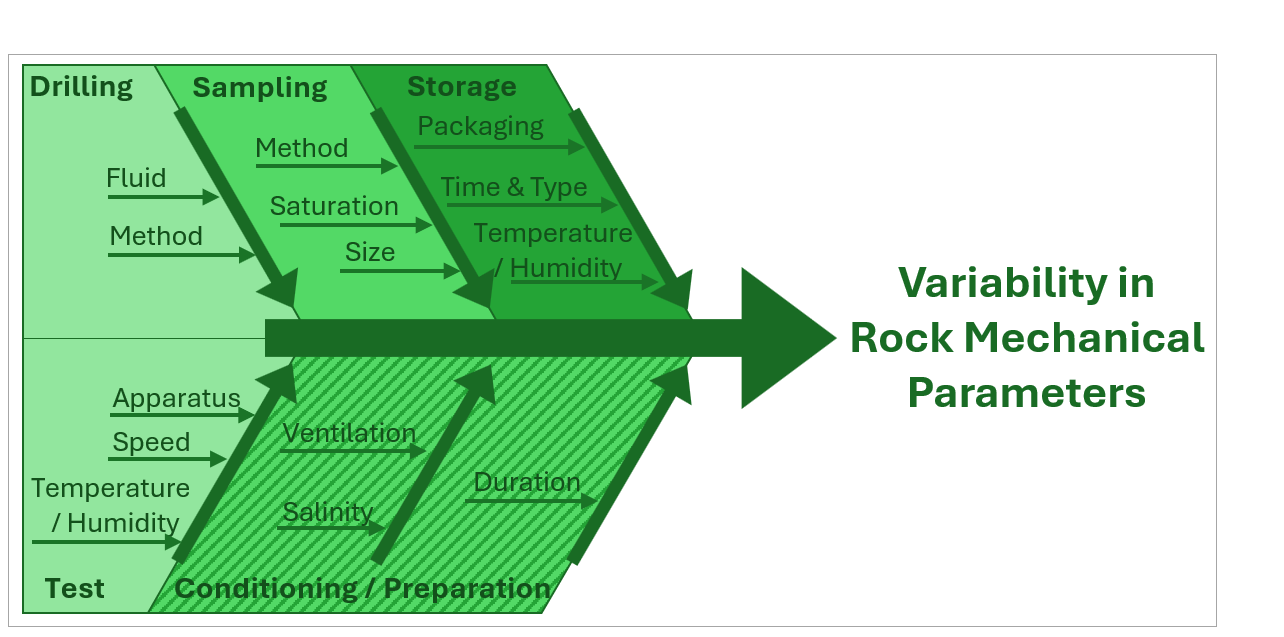
Die Modellierung realer Phänomene, wie thermische, hydraulische und mechanische (THM) Wechselwirkungen, stellt die komplexe Aufgabe dar, Systeme genau abzubilden und gleichzeitig Unsicherheiten in wesentlichen Parametern zu berücksichtigen. Diese Unsicherheiten resultieren häufig aus verschiedenen Datenungenauigkeiten, die durch Messgrenzen, Umweltvariabilität und die inhärente Heterogenität von Proben, insbesondere in geologischen Kontexten, beeinflusst werden. Einige Beispiele aus der nebenstehenden Abbildung sind etwa die Sensorpräzision, die Zusammensetzung der Proben, Erhaltungsmaßnahmen sowie schwankende Umweltbedingungen (z. B. Temperaturschwankungen), die alle zur Herausforderung beitragen, verlässliche Daten zu erfassen. Die Berücksichtigung dieser Faktoren ist entscheidend, um Modelle zu erstellen, die das Verhalten und die Wechselwirkungen innerhalb natürlicher Systeme realistisch widerspiegeln – insbesondere in Bereichen, die auf präzise Simulationen und Vorhersagen angewiesen sind.
Die folgenden Beispiele zeigen, wie Variabilität bzw. Unsicherheit in Materialeigenschaften die Genauigkeit und Zuverlässigkeit von Modellen beeinflusst:
¶ Beispiel 1: Scherfestigkeit
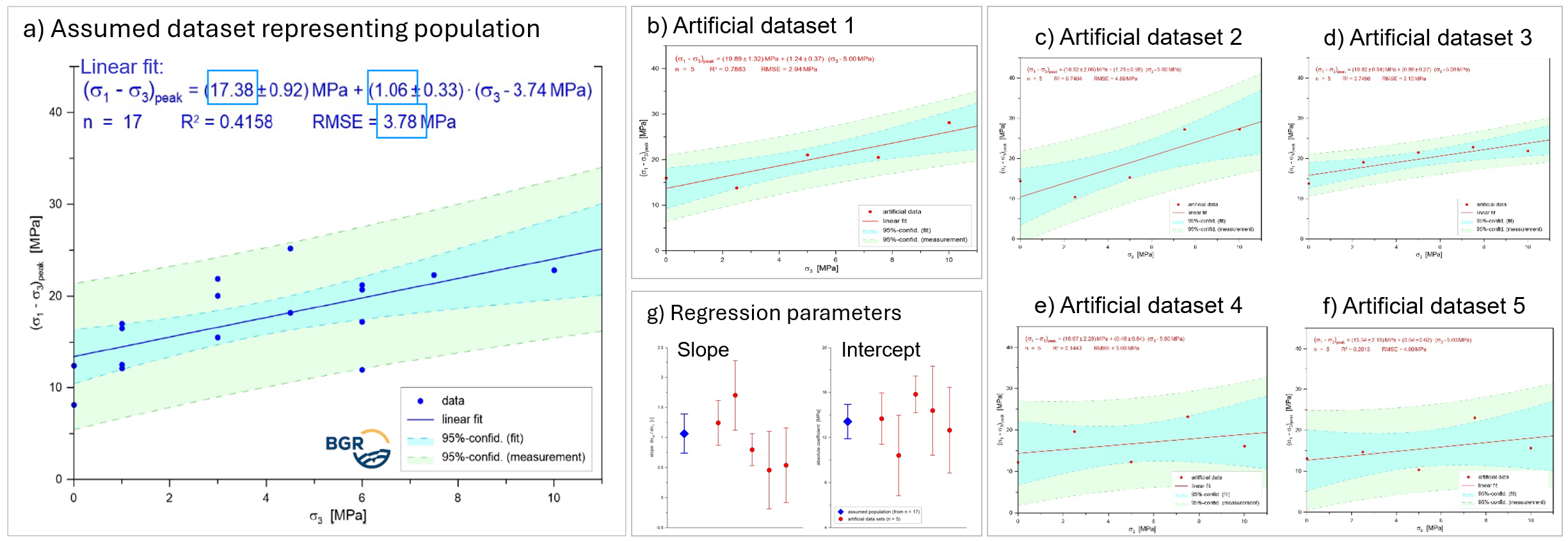
Die Scherfestigkeit ist ein wichtiger Parameter in der geomechanischen Modellierung, der beispielsweise aus Kohäsion (C) und dem Winkel der inneren Reibung (phi) bestimmt werden kann. Eine geringe Probenahmedichte (Diagramme b–f, die jeweils 5 Datenpunkte für 5 künstliche Datensätze auf Basis der realen Messdaten aus Diagramm a zeigen, welches 17 Datenpunkte für den Opalinuston enthält) kann erhebliche Auswirkungen auf die Zuverlässigkeit der linearen Regressionsresultate haben, was sich in großen Unsicherheiten bei Steigungs- und Achsenabschnittswerten widerspiegelt (Diagramm g).
¶ Beispiel 2: Porosität
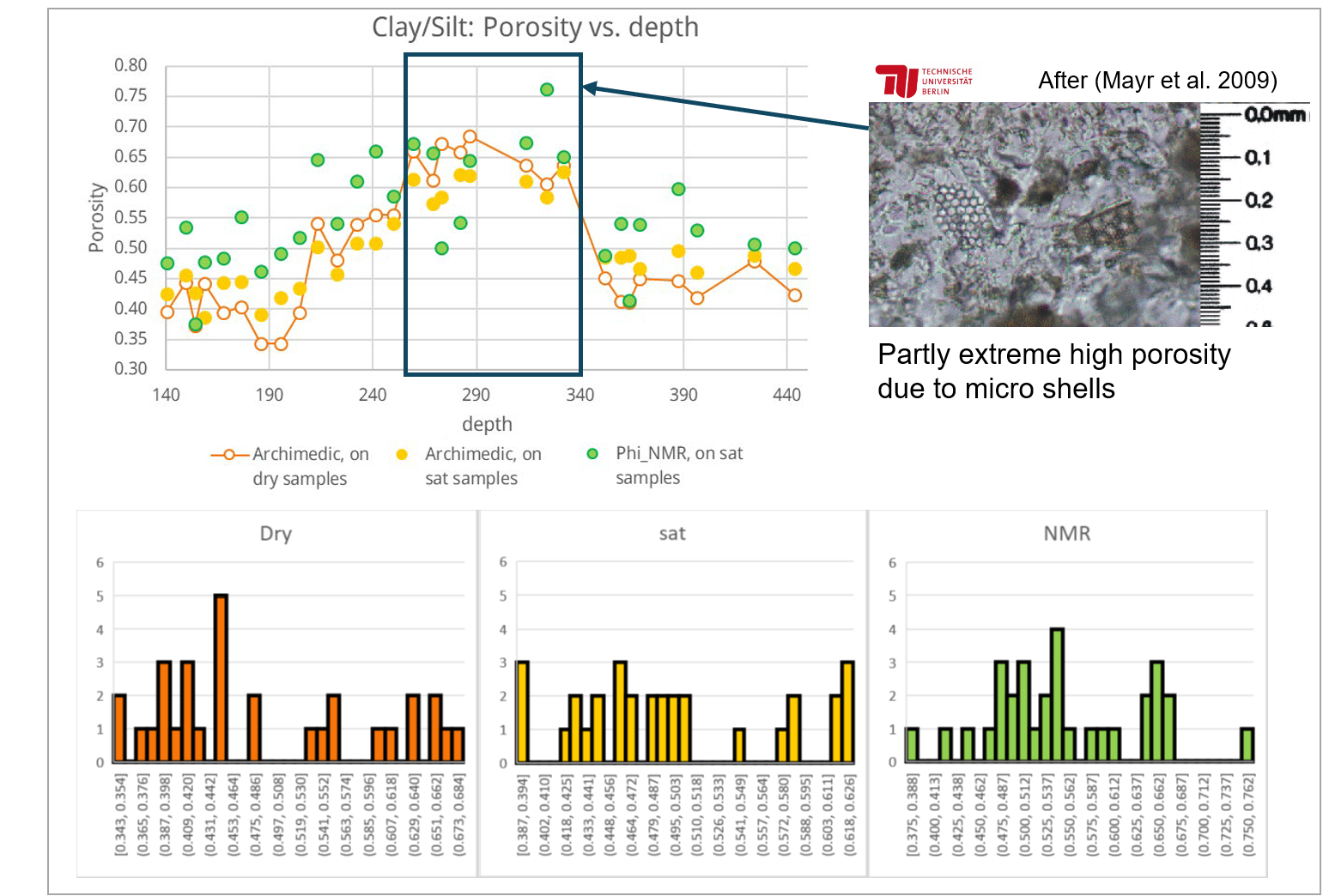
Porosität kann mit verschiedenen Techniken gemessen werden, z. B. durch Messungen an trockenen oder gesättigten Proben oder mittels Kernspinresonanz (NMR). Diese Verfahren unterscheiden sich nicht nur in der Probenvorbereitung, sondern auch im Zustand der Probe während der Messung (z. B. trockener versus gesättigter Zustand), was zu deutlich unterschiedlichen Messergebnissen führen kann (siehe Abbildung rechts):
- Messungen an trockenen Proben führten im Allgemeinen zu einer größeren Datenstreuung im Vergleich zu Messungen an gesättigten Proben.
- Die mittels Kernspinresonanz (NMR) bestimmte Porosität war tendenziell höher, möglicherweise aufgrund von gebundenem Wasser, das durch das Trocknen nicht entfernt werden kann.
Außerdem spielt die Zusammensetzung der Probe eine entscheidende Rolle für die Datenstreuung: Im hier gezeigten Beispiel führt das Vorhandensein von Karbonaten im mittleren Bereich aufgrund von Mikro-Schaleneinschlüssen zu extremen Porositätswerten während der Messung. Dies erschwert die statistische Analyse und die Integration in Modelle zusätzlich, da es häufig zu nicht-gauss'schen Verteilungen führt.
¶ Parametervariabilität in THM-Modellen
Um die geologische Integrität des Wirtsgesteins, das im Endlager im Wesentlichen als Barriere fungiert, zu bewerten, ist es entscheidend, das Verhalten des Endlagers über einen langen Zeitraum zu verstehen und vorherzusagen. Numerische Untersuchungen zur Barrierenintegrität beinhalten die Zuordnung von Materialeigenschaften zum Wirtsgestein für THM-Simulationen. Wären vollständige Informationen verfügbar, wären die Materialeigenschaften als Funktionen des Ortes bekannt, und Eigenschaften wie Inhomogenität und Anisotropie könnten durch räumlich variierende, tensorwertige Koeffizienten dargestellt werden. In der Realität jedoch sind Informationen über Variationen in der Struktur und den Eigenschaften der geologischen Barriere unvollständig, was folgende Fragen aufwirft:
- Auf welcher Skala muss Heterogenität berücksichtigt werden?
- Sind homogene Modelle mit zufälliger Parametrisierung geeignet, um diese Parametervariationen abzubilden?
¶ Methodik
Ein gängiger Ansatz zur Analyse der Auswirkungen von Heterogenität besteht darin, den Gesteinskörper abschnittsweise als homogen zu modellieren (z. B. geologische Schichten). Innerhalb dieser Abschnitte werden die betrachteten Materialparameter als Zufallsvariablen modelliert. Dieser Modellierungsansatz führt zu einer vollständig korrelierten Parameterbeschreibung an benachbarten Orten. Ein universelles Werkzeug zur Beschreibung von Zufälligkeiten mit einer allgemeineren Struktur ist die Nutzung von Zufallsfeldern, deren Realisierungen räumliche Funktionen sind und im Allgemeinen keine Konstanten darstellen – beispielsweise ein gaußsches Zufallsfeld, das durch seinen Mittelwert und seine Zwei-Punkt-Korrelationsfunktion bestimmt wird. In dieser Darstellung kann Anisotropie in zwei Formen auftreten:
- Statistische Anisotropie: Anisotropie, die in der statistischen Kovarianzstruktur vorhanden ist und zu unterschiedlichen Korrelationslängen entlang der Hauptachsen des Zufallsfeldes führt.;
- Physikalische Anisotropie: Anisotropie, die mit den thermischen, hydraulischen oder mechanischen Eigenschaften selbst verbunden ist und zu Zufallsfeldern führt, deren Realisierungen anisotrope Tensorfelder sind.
Wir stellen hier eine Vergleichsstudie für beide Fälle vor, indem wir für den ersten Fall unterschiedliche Korrelationslängen in parallel- und senkrechter Richtung wählen und für den zweiten Fall die dominierende Materialeigenschaft jedes Prozesses in THM-Simulationen als tensorwertiges Zufallsfeld beschreiben: die Wärmeleitfähigkeit für den thermischen Teil, die intrinsische Permeabilität für den hydraulischen Teil und die elastische Steifigkeit für den mechanischen Teil. Diese Eigenschaften spielen eine entscheidende Rolle bei der Bewertung thermisch induzierter Überdruckverhältnisse im Porenwasser und Spannungsänderungen (Buchwald et al., 2020; Chaudhry et al., 2021).
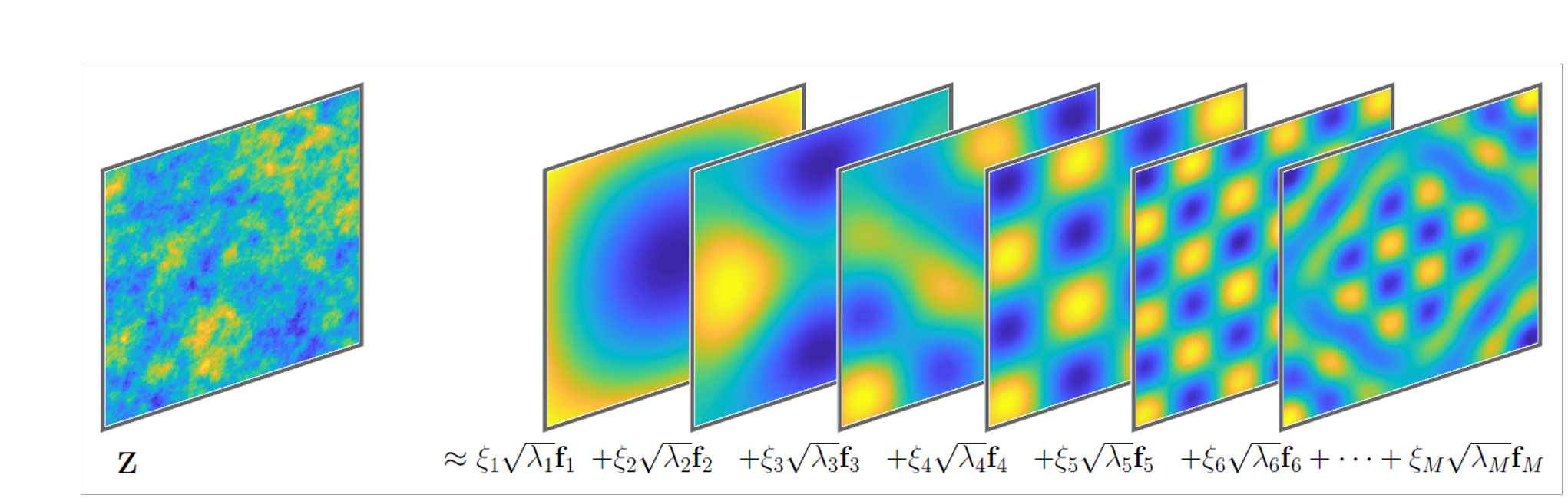
Zur Erzeugung der Zufallsfelder verwenden wir die Karhunen-Loève-Expansion, welche ein Zufallsfeld in eine Reihe orthogonaler Modi zerlegt: Die Eigenfunktionen erfassen die Variabilität des Feldes auf unterschiedlichen räumlichen Skalen, während die zugehörigen Eigenwerte den Anteil der Varianz quantifizieren, der durch diese Eigenfunktionen getragen wird. Die zur Beschreibung von Realisierungen gaußscher Zufallsfelder verwendete Formel lautet:
$${Z(x,\xi) = Z_{mean}(x) + \sum^M_{i=1}(\xi_i \sqrt{\lambda_i} f_i(x)) }$$
dabei ist Zmean(x) der Mittelwert des Feldes ξi ~ N(0,1), und fi sowie λi sind die Eigenfunktionen bzw. Eigenwerte des Kovarianzoperators, die numerisch durch Lösung des verallgemeinerten Eigenwertproblems bestimmt werden:
$${C f_i = \lambda_i M f_i}$$
$${ [C]_{i,j} = \int_D \phi_j(x) \int_D c(x,y) \phi_j(y) dy dx}$$
dabei ist φ die Basisfunktion und c(x,y) die Kernel- bzw. Kovarianzfunktion.
Die Lösung des oben beschriebenen Problems im Kontext von THM-Simulationen bringt mehrere Herausforderungen mit sich:
- Die Kovarianzmatrix [C]i,j beinhaltet Integrale über nicht-glatte Kovarianzfunktionen c(x,y), was die numerische Integration erschwert und zu Genauigkeitsproblemen führen kann.
- Die Kovarianzmatrix [C]i,j ist voll besetzt (dicht) und hat die Größe N × N, wobei N die Anzahl der Freiheitsgrade ist. Dies führt zu hohem Speicherbedarf und rechenintensiven Matrix-Vektor-Produkten.
- Zur Bestimmung der Eigenfunktionen und Eigenwerte wird ein Eigenwertlöser benötigt, dessen Anwendung bei großen Systemen sehr rechenaufwendig ist.
Wir begegnen diesen Herausforderungen durch folgende Maßnahmen:
- Zur Abschwächung des Singularitätsproblems verwenden wir das Sauter-Schwab-Quadraturverfahren (Sauter und Schwab, 2011), das speziell für Integrale mit schwach-singulären Kernen entwickelt wurde.
- Zur Reduzierung des Rechenaufwands bei der Lösung des Problems führen wir eine hierarchische Matrixapproximation der Kovarianzmatrix ein. Diese Methode senkt den Aufwand für Matrixaufbau und Matrix-Vektor-Multiplikationen von O(N2) auf O(N logN).
- Für das Eigenwertproblem implementieren wir den Thick-Restart-Lanczos-Eigensolver (Wu und Simon, 2000), der für große, dünnbesetzte oder hierarchisch strukturierte Matrizen besonders effizient ist.
¶ Auswirkungen von Inhomogenität und Anisotropie
Die Fallstudie zur Untersuchung der Auswirkungen von Anisotropie und Inhomogenität basiert auf einem Benchmark-artigen Aufbau aus früheren Arbeiten (Chaudhry et al. 2021, Buchwald et al. 2020, Pitz et al. 2023): ein kreisförmiges 2D-Gebiet mit einem Durchmesser von 100 m und einem zentralen kreisförmigen Hohlraum, der die eingebrachte hochradioaktive Abfallzelle darstellt (Durchmesser 2,48 m).
Es werden drei Eingangsparameter mit hoher Unsicherheit identifiziert: Wärmeleitfähigkeit (λ), intrinsische Permeabilität (k) und Elastizitätsmodul (E). Um die Auswirkungen von Inhomogenität und Anisotropie zu bewerten, werden diese drei Parameter so definiert, dass sie entsprechendes Verhalten widerspiegeln. Zur besseren Verständlichkeit unterscheiden wir zwischen materieller und statistischer Anisotropie:
- Materielle Anisotropie: Bezieht sich auf das intrinsische, richtungsabhängige Verhalten einer physikalischen Materialeigenschaft. Zum Beispiel kann die intrinsische Permeabilität je nach Ausrichtung (parallel vs. senkrecht zur Schichtungsebene im Gestein) variieren. Sie wird durch tensorwertige Zufallsfelder modelliert, wobei eine Realisierung symmetrisch positiv-definiter Matrizen erzeugt wird, die entlang spezifischer Hauptachsen ausgerichtet sind.
- Statistische Anisotropie: Beschreibt Anisotropie in der Korrelationsstruktur der Zufallsfelder, welche die Materialeigenschaft repräsentieren. Das bedeutet, dass die räumliche Variabilität der Eigenschaften richtungsabhängig ist, was zu unterschiedlichen Korrelationslängen entlang der Hauptachsen führt (z. B. längere Korrelation entlang der Schichtungsebene als senkrecht dazu). Dies wird durch Anpassung der Kovarianzfunktion modelliert, wobei anisotrope Skalierungsfaktoren eingeführt werden, die die Dehnung der Variabilität in den jeweiligen Richtungen beschreiben.
Eine Übersicht der etablierten Szenarien ist in Tabelle X dargestellt. In den ersten sechs homogenen Fällen wurden räumlich konstante Werte für die drei unsicheren Eingaben verwendet. In den mit „Extrem“ bezeichneten Fällen wurden alle acht Kombinationen der drei Extremwerte Ext ∈ {Min, Max} simuliert. In den mit „Zufällig“ bezeichneten Fällen wurden die räumlich konstanten Werte der drei Eingangsparameter zufällig aus ihren Wahrscheinlichkeitsverteilungen gezogen. Die letzten vier Fälle verwendeten räumlich veränderliche Zufallsfelder für die drei Eingangsgrößen.
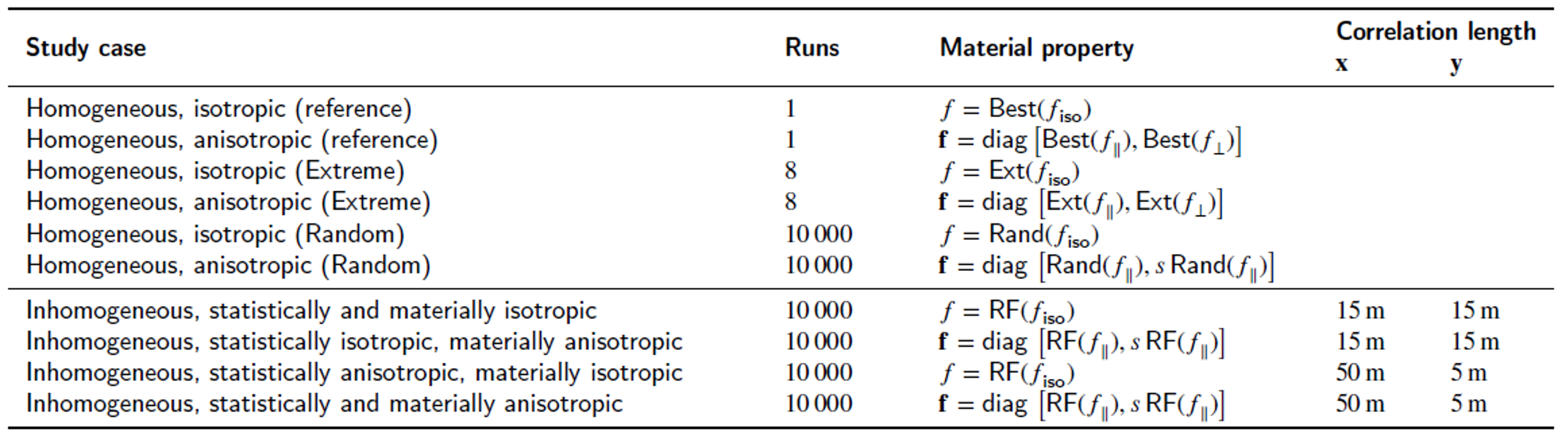
Da in dieser Studie mehrere Fälle gezielt entworfen wurden, um die Auswirkungen von Inhomogenität und Anisotropie zu isolieren, werden die Einzelheiten zu den jeweiligen Fällen parallel diskutiert, um die jeweiligen Einflüsse hervorzuheben. Eine kurze Zusammenfassung der relevantesten Ergebnisse ist nachfolgend aufgeführt. Für weitere Details wird auf den Artikel von Chaudhry et al. 2025 verwiesen.
¶ Homogene Fälle:
- Isotrope vs. Anisotrope Ergebnisse: Bei isotropen Fällen zeigen die Ergebnisse radiale Symmetrie in Temperatur-, Fluiddruck-, Verschiebungs- und Spannungsverläufen. Anisotrope Fälle hingegen weisen elliptische Konturen der Ausgangsgrößen auf, wobei die Hauptachsen von der dominanten Materialrichtung abhängen. Diese Umkehrung der Achsen in verschiedenen Radien ist auf komplexe Kopplungseffekte zurückzuführen.
- Extremfälle: Die Wärmeleitfähigkeit beeinflusst maßgeblich die Temperatur. Andere Parameter (Permeabilität, Elastizitätsmodul) zeigen sekundäre Effekte, die durch Kopplungsmechanismen angetrieben werden. Druck und Verschiebung zeigen komplexe Wechselwirkungen, wobei extreme Kombinationen der Parameter zu lokalisierten Spitzen und Abweichungen bei den Antwortgrößen führen.
- Zufällige Fälle: Die Variabilität der Ausgangsgrößen ist bei zufälligen Fällen (95%-Bandbreite) geringer als bei Extremfällen, mit Ausnahme der Temperatur, die stärker linear von der Wärmeleitfähigkeit abhängt. Gekoppelte Eingabe-Ausgabe-Beziehungen führen zu Schwankungen in den Ausgabebandbreiten, die durch einfache Zufallsstichproben nicht vollständig erfasst werden.
¶ Inhomogene Fälle:
- Statistisch und materiell Isotropie: Die Einbindung von Zufallsfeldern führt zu räumlicher Variabilität und erzeugt glattere Übergänge in den Temperatur-, Druck- und Verschiebungsfeldern. Im Vergleich zu homogenen Modellen verringert die Inhomogenität scharfe Spitzen in den Spannungsantworten, was den Mittelungseffekt räumlicher Zufälligkeit widerspiegelt.
- Statistische Anisotropie: Anisotrope Korrelationslängen (z. B. 50 m in x-Richtung vs. 5 m in y-Richtung) führen zu gestreckten oder gestauchten Antwortfeldern. Spannungsindikatoren zeigen anisotropiebedingte Asymmetrien in der von-Mises-Spannung und im effektiven hydrostatischen Druck..
- Materielle Anisotropie: Variabilität in Materialeigenschaften (z. B. anisotrope Permeabilität und Wärmeleitfähigkeit) erzeugt ausgeprägtere Richtungsabhängigkeiten in Strömungs- und Spannungsfeldern. Beobachtete Unterschiede bestätigen die Notwendigkeit, materielle Anisotropie in Vorhersagemodellen zu berücksichtigen, um Scher- und Zugversagensrisiken realitätsnah abzubilden.
- Kombinierte Anisotropie und Inhomogenität: Die Kombination aus statistischer und materieller Anisotropie mit Zufallsfeldern liefert die realistischsten Ergebnisse. Die Resultate stimmen gut mit dem erwarteten Verhalten in komplexen geologischen Medien überein und spiegeln das Zusammenspiel von räumlicher Variabilität und richtungsabhängigen Materialreaktionen wider.
¶ Literaturverzeichnis
- D. Jaeggi, P. Bossart, L. Wymann (2014). Kompilation der lithologischen Variabilität und Eigenschaften des Opalinus-Ton im Felslabor Mont Terri. Expertenbericht im Rahmen der Beurteilung des Vorschlags von mindestens zwei geologischen Standortgebieten pro Lagertyp, Etappe 2, Sachplan geologische Tiefenlager.
- A. A. Chaudhry, C. Zhang, O. G. Ernst, T. Nagel (2025). Effects of inhomogeneity and statistical and material anisotropy on THM simulations. Reliability Engineering and System Safety, 260. DOI:10.1016/j.ress.2025.110921