¶ Erweitertes Bayes’sches Netzwerk
¶ Methodik
Das Projekt verwendet erweiterte Bayes’sche Netzwerke (eBNs) mit unpräzisen Wahrscheinlichkeiten zur Zuverlässigkeitsbewertung. Wichtige Merkmale des gewählten Rahmens sind:
- Eine direkte visuelle Darstellung des Problems, welche die graphenbasierte Struktur des Werkzeugs hervorhebt
- Die Möglichkeit, Expertenwissen aus verschiedenen Fachbereichen in einem einzigen Rahmen zu integrieren
- Die Verwendung von Eltern-Kind-Beziehungen, um die Wahrscheinlichkeiten der Zustände eines Knotens leichter zu definieren; diese werden in bedingten Wahrscheinlichkeitsmatrizen (CPTs) erfasst
- Die Möglichkeit, Knoten über Wahrscheinlichkeitsdichtefunktionen (pdfs) zu beschreiben – unter Anwendung struktureller Zuverlässigkeitsmethoden zur Berechnung der CPTs
- Die Möglichkeit, Knoten über Intervalle oder p-Boxen zu beschreiben – unter Verwendung von Double-Loop-Simulationen zur Bewertung der CPTs
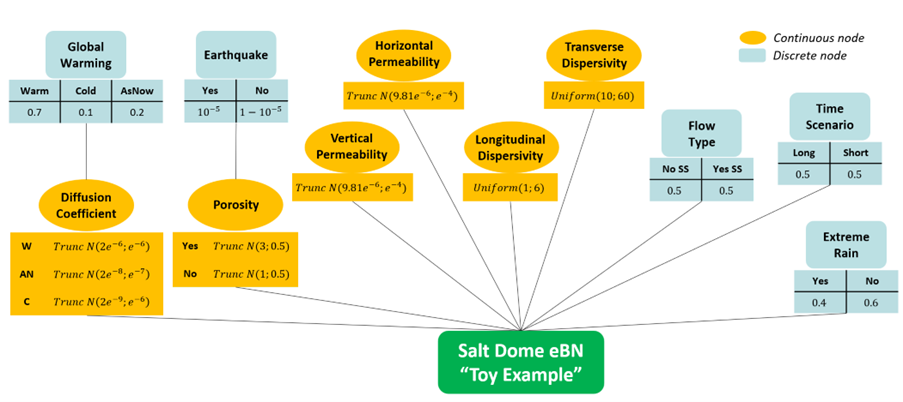
Ein theoretisches Beispiel für das entwickelte eBN ist in der obigen Abbildung dargestellt. Die hier gezeigten Werte dienen ausschließlich einem hypothetischen Beispiel; bei einer Anwendung im Feld würden Wahrscheinlichkeitswerte und Zusammenhänge auf Grundlage von Messdaten, Literaturrecherchen und Expertenwissen definiert. Diskrete Knoten repräsentieren Ereignisse mit klar abgegrenzten Ausgängen, die durch diskrete Wahrscheinlichkeiten beschrieben werden. Ein Beispiel ist der Knoten „Erdbeben“, der zwei mögliche Ausgänge hat – entweder tritt es ein (Ausgang „ja“) mit einer Wahrscheinlichkeit von 10⁻⁵ oder es tritt nicht ein („nein“) mit einer Wahrscheinlichkeit von 1 − 10⁻⁵. Kontinuierliche Knoten sind mit Eigenschaften verbunden, deren Ausgänge/Werte über Wahrscheinlichkeitsdichtefunktionen (pdfs) beschrieben werden. Ein Beispiel ist die Materialeigenschaft der vertikalen Permeabilität (Knoten „Vertikale Permeabilität“), die durch eine abgeschnittene Normalverteilung mit einem Mittelwert von 9,81 × 10⁻⁶ und einer Standardabweichung von 1 × 10⁻⁴ beschrieben wird. Kindknoten (z. B. „Porosität“), deren Ergebnisse vom Ausgang ihrer Elternknoten (z. B. „Erdbeben“) abhängen, können sowohl diskret als auch kontinuierlich definiert sein.
Das entwickelte Werkzeug ist im folgenden Repository zum Download verfügbar.
¶ Ergebnisse
Das eBN-Rahmenwerk zeigte die Fähigkeit:
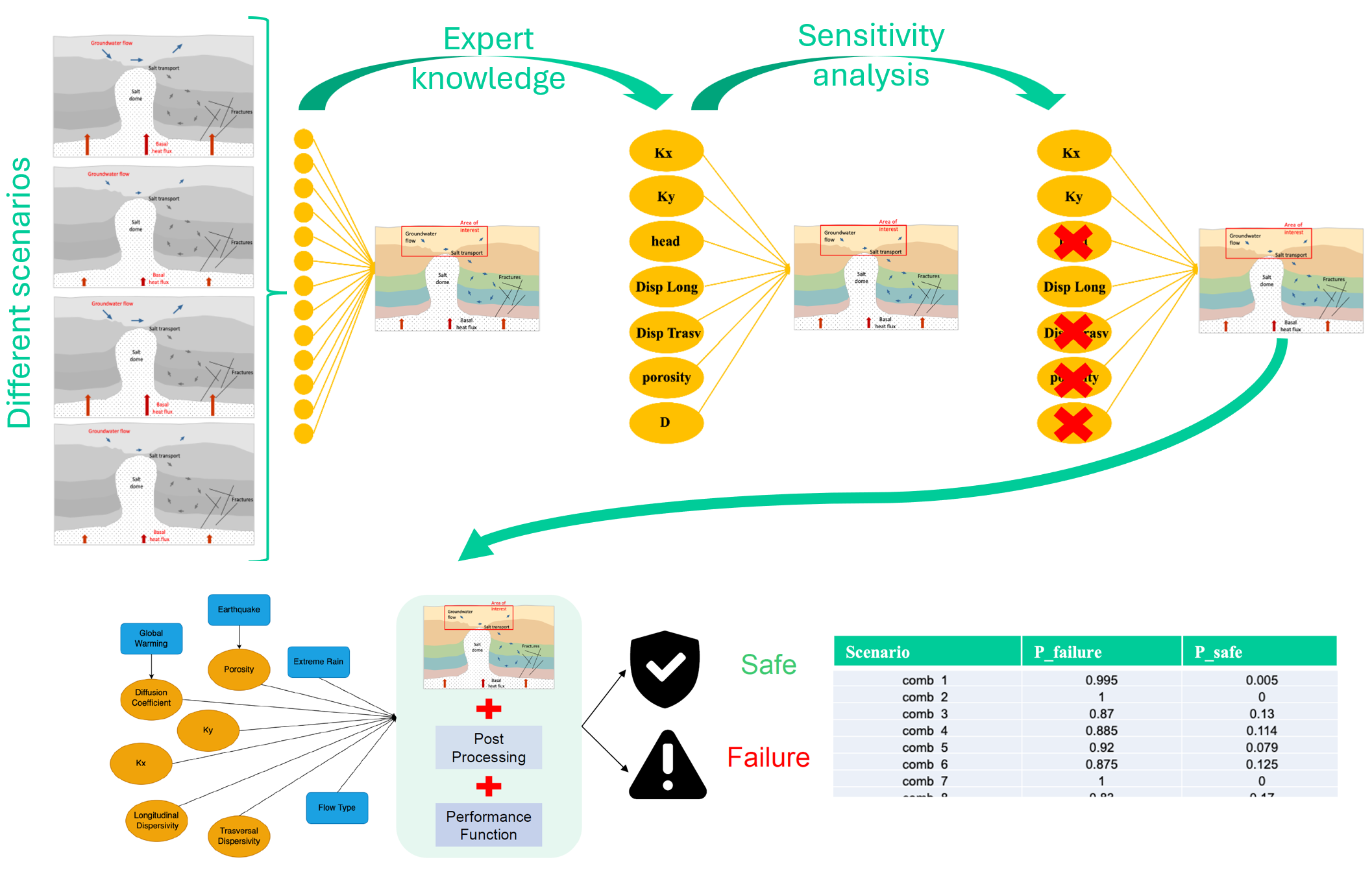
¶ 1. Risikobewertungen unter Einbindung externer Modelle durchzuführen.
Anforderungen an ein solches Werkzeug:
- Unterstützung mehrerer Szenarien: Expertenbasiertes Wissen zur Parameteridentifikation; Sensitivitätsanalysen zur Verbesserung der Recheneffizienz
- Fähigkeit zur Entscheidungsunterstützung durch „Was-wäre-wenn“-Analysen
- Berücksichtigung aleatorischer Unsicherheiten durch kontinuierliche Knotendefinition
- Durchführung Bayes‘scher Updates
- Durchführung von Inferenzanalysen (Prognose und Diagnose)
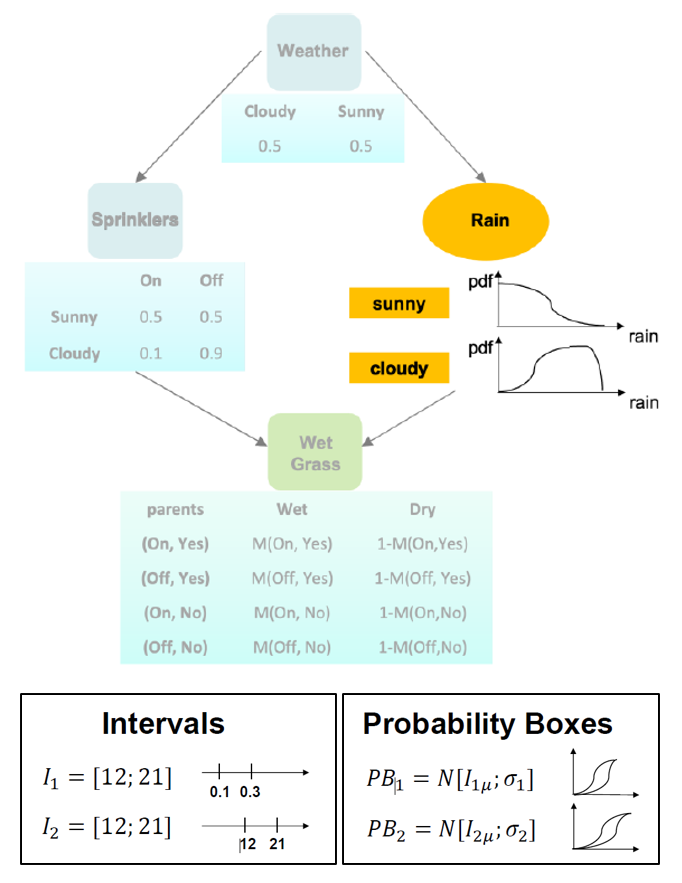
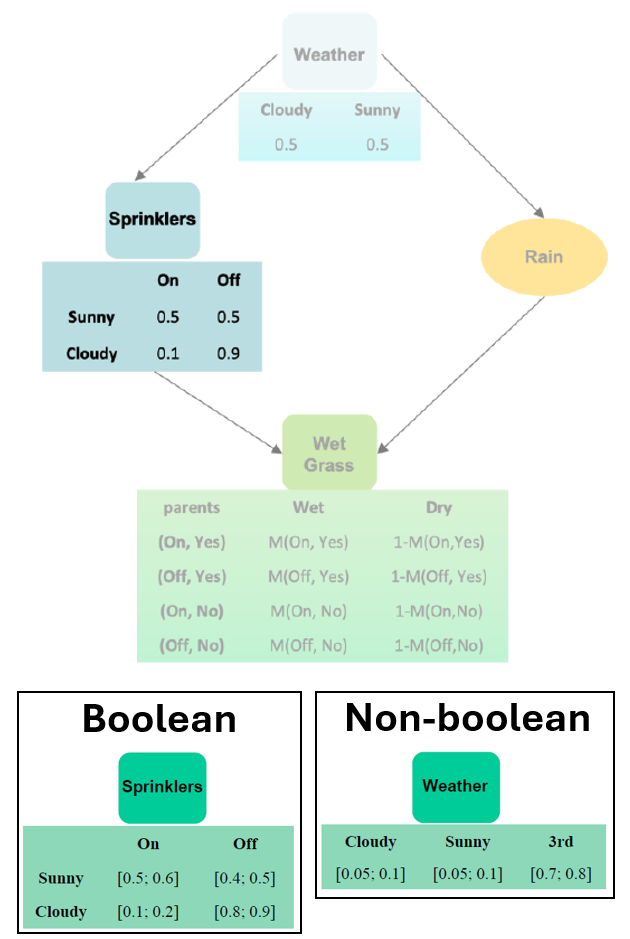
¶ 2. Umgang mit unpräzisen Wahrscheinlichkeiten
Unpräzise Wahrscheinlichkeiten treten auf, wenn eine exakte Beschreibung der Wahrscheinlichkeit (diskrete Werte für diskrete Knoten / präzise Wahrscheinlichkeitsverteilungen für kontinuierliche Knoten) unter unsicheren Bedingungen erfolgt – z. B. bei geringer Datenverfügbarkeit, begrenzten Messungen oder subjektiver Dateninterpretation.
| Unpräziser kontinuierlicher Knoten | Unpräziser diskreter Knoten |
 |
 |
|
Unpräzise Bedingungen:
Bewertungsfolgen:
Inferenzfolgen:
|
Unpräzise Bedingungen:
Keine bekannten Bewertungsfolgen. Inferenzfolgen:
|
¶ 3. Implementierung fortgeschrittener Algorithmen zur Weitergabe von Unschärfe im eBN-Rahmen
Fortgeschrittene Algorithmen wurden ausgewählt, um:
- die Recheneffizienz aller graphenbasierten Operationen durch den Einsatz einer Adjazenzmatrix zu verbessern
- die Recheneffizienz bei Mehrszenarienanalysen durch nicht-intrusive unpräzise stochastische Simulation (NISS) sowie durch kollaborative und adaptive Bayes’sche Optimierung (CABO) zu steigern
- ein dynamisches Bayes’sches Netzwerk zu integrieren, um sequenzielle Daten (z. B. Zeitreihen) abbilden zu können
Dieser Abschnitt befindet sich derzeit in Bearbeitung.