¶ Enhanced Bayesian Networks
¶ Methodology
The project employs Enhanced Bayesian Networks (eBNs) with imprecise probabilities for reliability assessments. Key features of selected framework include:
- A direct visual representation of the problem highlighted the tool’s graph-based nature
- Possibility of integrate in a single framework expert knowledge from different fields
- Usage of parent-child relation to easier define the probabilities of a node’s states which are collected in Conditional Probability Tables (CPTs)
- Possibility of defining nodes described by probability distribution functions (pdfs) through the employment of structural reliability methods for the evaluation of the CPTs
- Possibility of defining nodes described by intervals or p-boxes through the employment of Double Loop simulation for the evaluation of the CPTs.
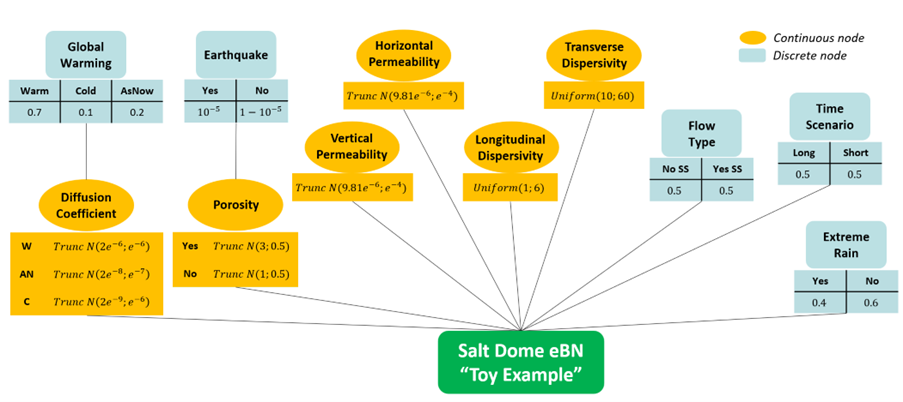
A theoretical example for the developed eBN is illustrated in the figure above. The values presented here are purely for a hypothetical case; field application would define probability values and relations based on measurement data, literature research and expert knowledge. Discrete nodes represent events that have distinct outcomes characterized with discrete probability value: an example would be the node “Earthquake” which has two possible outcome - either it happens (outcome “yes”) with a probability of 10-5 or it doesn't (outcome “no”) with a probability of 1 - 10-5. Continuous nodes are connected to properties with outcomes/values given by probability density functions, e.g. the material property of vertical permeability (the node “Vertical Permeability”) represented with a truncated normal distribution with a mean of 9.81e-6 and standard normal distribution of 1e-4. Child nodes (the node “Porosity”) that have conditional outcomes dependent on the outcome of their parents (the node “Earthquake”) can have either discrete or continuous node definitions.
The developed tool is available for download on this repository.
¶ Results
The eBN framework demonstrated the ability to:
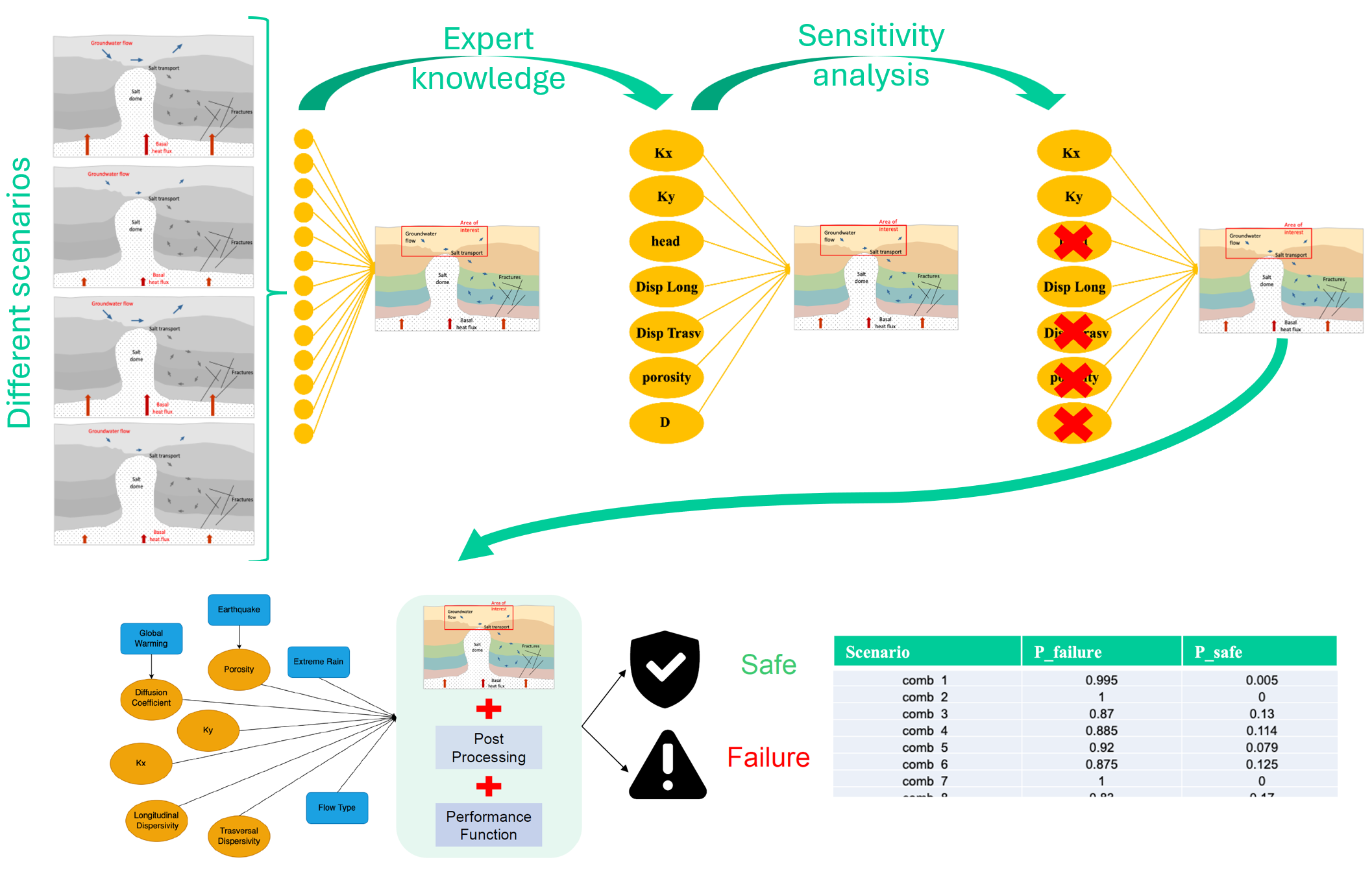
¶ 1. Provide risk assessment with external models
The requirements for such a tool:
- Can handle Multiple scenario analysis: expert-based knowledge for parameter identification; sensitivity analysis for improving computational efficiency
- Capable to enhance decision-making process through “what-if” analysis
- Considers aleatoric uncertainties through continuous node definition
- Performs Bayesian update
- Includes inference analysis (prognosis and diagnosis)
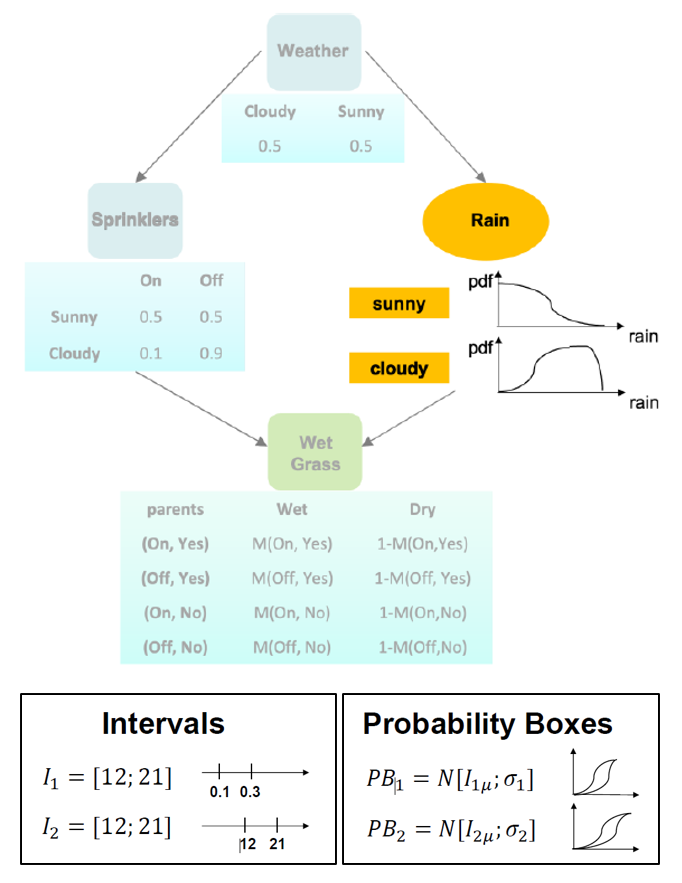
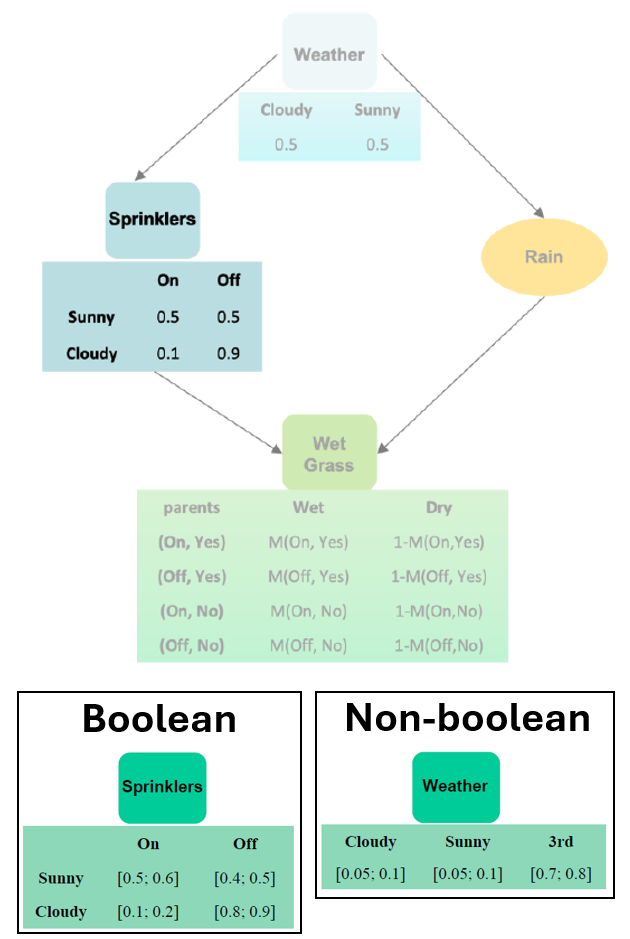
¶ 2. Manage imprecise probabilities
Imprecise probabilities can occur when precise description of probability (discrete values for discrete nodes/precise probability distributions for continuous nodes) is given under imprecise conditions - e.g. sparse data availability, limited measurements, subjective data interpretation.
| Imprecise continuous node | Imprecise discrete node |
 |
 |
|
Imprecise conditions:
Evaluation consequences:
Inference consequences:
|
Imprecise conditions:
No known evaluation consequence. Inference consequences:
|
¶ 3. Implement advanced algorithms to propagate imprecision in the eBN framework
Advanced algorithms were selected in order to:
- Improve computational efficiency of all graph-based operation through adjacency matrix
- Improve computational efficiency of the multiple scenario analysis through non-intrusive imprecise stochastic simulation (NISS) and collaborative and adaptive Bayesian optimization (CABO)
- Add dynamic Bayesian network to handle sequence-type data (e.g. time series)
This section is currently work-in-progress.